Excel Varyans Hesaplama: Örneklerle Rehber
Varyans, bir dizi sayının ne kadar dağıldığını gösteren bir istatistiksel ölçüdür. Finans, bilim ve birçok diğer alanda kritik bir kavramdır ve veri setlerimizdeki değişkenliği veya dağılımı anlamamıza yardımcı olur. Excel, varyans hesaplamak için basit bir yol sunarak hem yeni başlayanlar hem de ileri düzey kullanıcılar için erişilebilir hale getirir. Bu makalede, net örneklerle bunun nasıl yapılacağını inceleyeceğiz.
Varyans nedir?
Excel varyans fonksiyonlarına giriş
Excel'de varyans nasıl hesaplanır?
- VAR.S vs VAR.P – Örnek veya popülasyondan varyans hesaplama
- VAR.S vs VARA – Metinleri ve mantıksal değerleri dahil ederek veya hariç tutarak varyans hesaplama
Varyans vs Standart sapma
Varyans nedir?
Varyans, bir veri setindeki sayıların ortalamadan (veya ortalama) ne kadar farklı olduğunu tanımlayan bir istatistik terimidir. Esas olarak, sayıların ne kadar dağıldığını ölçer. Varyansı anlamadaki temel bir nokta, bu kavramın bir değer kümesi içindeki değişim veya dağılım derecesini nicelendirdiğini fark etmektir. Yüksek varyans, sayıların dağıldığı anlamına gelir; düşük varyans ise sayıların ortalamaya yakın bir şekilde toplandığı anlamına gelir.
Varyansı Açıklamak İçin Basit Bir Örnek:
Senaryo: Matematik sınavından alınan puanlarla beş öğrencisi olan bir sınıf düşünün. Puanlar 90, 92, 88, 91 ve 89 olsun.
Ortalamayı Hesaplayın: İlk olarak, ortalama (mean) puanı buluruz. Ortalama şu şekildedir:
Varyansı Hesaplayın: Ardından, varyansı hesaplarız. Bu, her puandan ortalamayı çıkarıp sonucu karelerine alma ve ardından bu karelerin ortalamasını alma işlemlerini içerir.
= [0 + 4 + 4 + 1 + 1] / 5
= 10 / 5
= 2
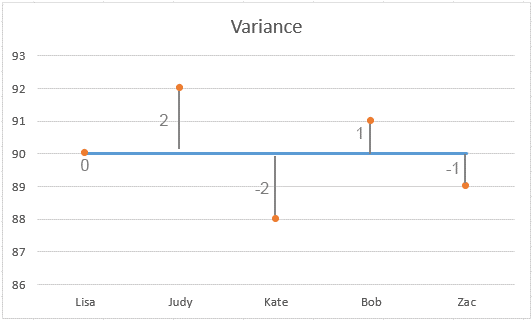
Puanların dağılımını gösteren bir grafik:
Sonucu Anlama:
Düşük Varyans: Bu örnekte, varyans 2'dir. Bu, nispeten düşük bir değerdir ve çoğu puanın ortalamaya (90) yakın olduğunu gösterir. Varyans ne kadar düşükse, setteki bireysel sayılar o kadar ortalama değere yakındır.
Sıfır Varyans: Eğer tüm öğrenciler tam olarak 90 almış olsaydı, varyans 0 olurdu ve bu da hiçbir değişkenlik olmadığını gösterirdi. Her puan aynı olurdu.
Yüksek Varyans: Tersine, daha yüksek bir varyans, puanların ortalamadan daha fazla dağıldığı ve öğrencilerin performansında daha fazla değişkenlik olduğunu gösterir.
Özetle, varyans, puanların (veya herhangi bir sayı setinin) ortalama değerden ne kadar saptığını nicelendirmemize yardımcı olan bir sayısal değer sağlar ve verilerin tutarlılığı veya değişkenliği hakkında bilgi verir.
Excel varyans fonksiyonlarına giriş
Excel, farklı veri senaryoları için tasarlanmış çeşitli fonksiyonlar sunarak varyans hesaplamak için araçlar sağlar.
Bu fonksiyonları anlamak, doğru istatistiksel analiz için çok önemlidir.
VAR.S (Örnek Varyans, yalnızca sayılar):
- Bir popülasyonun örneğine dayalı varyansı hesaplar.
- Tüm veri seti hakkında çıkarım yapmak için bir alt küme analiz ederken en iyi şekilde kullanılır.
VAR.P (Popülasyon Varyansı, yalnızca sayılar):
- Tüm popülasyon için varyansı hesaplar.
- Tam veriye sahip olduğunuzda ve yalnızca bir örnek olmadığında idealdir.
VARA (Örnek Varyans, metin ve mantıksal değerleri dahil):
- VAR.S'ye benzer ancak metin ve mantıksal değerleri de hesaba katar (metin 0, DOĞRU 1, YANLIŞ 0 olarak kabul edilir).
- Veri setiniz sayılar, metin ve mantıksal değerler gibi karışık türler içerdiğinde faydalıdır.
VARPA (Popülasyon Varyansı, metin ve mantıksal değerleri dahil):
- VARA'nın popülasyon varyansı sürümüdür.
- Tüm popülasyon için varyans hesabında tüm türdeki verileri içerir.
VAR (Eski Örnek Varyans):
- VAR.S'nin eski bir sürümüdür ve özellikle Excel 2007 ve önceki sürümlerde kullanılmıştır.
- Tutarlılık ve açıklık açısından yeni sürümlerde VAR.S kullanılması önerilir.
VARP (Eski Popülasyon Varyansı):
- VAR.P'nin eski sürümüdür.
- VAR gibi, yeni Excel sürümlerinde VAR.P kullanılması önerilir.
Farklar ve Karşılaştırmalar:
- Örnek vs. Popülasyon: VAR.S ve VARA örnekler içindir, VAR.P ve VARPA ise tüm popülasyon içindir.
- Veri Türü Dikkate Alınması: VARA ve VARPA, VAR.S ve VAR.P'nin aksine metin ve mantıksal değerleri hesaba katar.
- Eski vs. Modern Fonksiyonlar: VAR ve VARP eski fonksiyonlardır ve mevcut Excel sürümleriyle daha iyi uyumluluk için VAR.S ve VAR.P ile değiştirilebilirler.
Karşılaştırma Tablosu:
| Fonksiyon | Dikkate Alınan Veri Türü | Popülasyon veya Örnek | Kullanım Durumu |
| VAR.S | Yalnızca Sayılar | Örnek | Sayısal veriler için örnek varyans |
| VAR.P | Yalnızca Sayılar | Popülasyon | Sayılar için popülasyon varyansı |
| VARA | Sayılar, Metin, Mantıksal Değerler | Örnek | Karışık veriler için örnek varyans |
| VARPA | Sayılar, Metin, Mantıksal Değerler | Popülasyon | Karışık veriler için popülasyon varyansı |
| VAR | Yalnızca Sayılar | Örnek | Örnek varyans için eski fonksiyon |
| VARP | Yalnızca Sayılar | Popülasyon | Popüler için eski fonksiyon |

Kutools AI ile Excel Sihirini Keşfedin
- Akıllı Yürütme: Hücre işlemleri gerçekleştirin, verileri analiz edin ve grafikler oluşturun—tümü basit komutlarla sürülür.
- Özel Formüller: İş akışlarınızı hızlandırmak için özel formüller oluşturun.
- VBA Kodlama: VBA kodunu kolayca yazın ve uygulayın.
- Formül Yorumlama: Karmaşık formülleri kolayca anlayın.
- Metin Çevirisi: Elektronik tablolarınız içindeki dil engellerini aşın.
Excel'de varyans nasıl hesaplanır?
Bu bölümde, Excel'de varyans hesaplamayı göstermek için iki örnek sunacağız ve farklı varyans fonksiyonları arasındaki farkları açıklayacağız. Sonuç olarak, farklı varyans fonksiyonlarının aynı örnek veri için tamamen farklı sonuçlar verdiğini göreceksiniz.
VAR.S vs VAR.P – Örnek veya popülasyondan varyans hesaplama
Senaryo: Büyük bir popülasyonun küçük bir örneği için varyans hesaplamak vs tüm popülasyon için varyans hesaplamak.
Örnek: A2:A12 sütunundaki değerler için varyansı hesaplayın.
Formül: Boş bir hücre seçin ve ihtiyacınıza göre aşağıdaki formüllerden birini yazın, ardından Enter tuşuna basın.
Büyük bir veri setinin örnekleri için varyansları alma (A2:A12'deki değerler büyük bir veri setinin parçaları olduğu varsayımıyla)
=VAR.S(A2:A12)
Tüm popülasyon için varyansı alma (A2:A12'deki değerlerin tüm veri seti olduğu varsayımıyla)
=VAR.P(A2:A12)
Gördüğünüz gibi, aynı değerler ancak farklı varyans fonksiyonları kullanıldığında farklı sonuçlar elde edilir.
Neden VAR.S ve VAR.P sonuçları farklı?
- VAR.S: Bu fonksiyon, veri setiniz daha büyük bir popülasyonun bir örneğini temsil ettiğinde kullanılır. "n-1" yöntemine dayanarak varyansı hesaplar, burada "n", örnekteki veri noktası sayısıdır. "n-1" yerine "n"'nin paydası olarak kullanılması, örnekteki yanlılığı düzeltir ve popülasyon varyansının yansız bir tahminini sağlar. Örnek verilerinin örnek ortalaması etrafındaki değişkenliğini tahmin eder.
- VAR.P: Bu fonksiyon, veri setiniz yalnızca bir örnek değil, tüm bir popülasyonu temsil ettiğinde kullanılır. "n" yöntemine dayanarak varyansı hesaplar, burada "n", popülasyondaki veri noktası sayısıdır. Veri setinin tüm popülasyonu kapsadığını varsayar, bu nedenle VAR.S'de olduğu gibi yanlılığı düzeltmeye gerek yoktur.
- Özetle, temel fark formülün paydasındadır. VAR.S, verilerin örnek doğasını hesaba katmak için "n-1" kullanırken, VAR.P, örneklemenin söz konusu olmadığı popülasyon verileri için "n" kullanır. Veri setiniz ve bu setin bir örnek mi yoksa tam bir popülasyon mu olduğuna bağlı olarak, varyansı hesaplamak için uygun fonksiyonu seçmelisiniz.
VAR.S vs VARA – Metinleri ve mantıksal değerleri dahil ederek veya hariç tutarak varyans hesaplama
Senaryo: Varyans hesaplamasına mantıksal değerleri ve metinleri dahil edip etmeyeceğinizi karar vermek.
Örnek: A2:A12 sütunundaki değerler için varyansı hesaplayın.
Formül: Boş bir hücre seçin ve ihtiyacınıza göre aşağıdaki formüllerden birini yazın, ardından Enter tuşuna basın.
Metinleri ve mantıksal değerleri göz ardı ederek büyük bir veri setinin örnekleri için varyansları alma.
=VAR.S(A2:A12)
Metinleri ve mantıksal değerleri dahil ederek büyük bir veri setinin örnekleri için varyansı alma.
=VARA(A2:A12)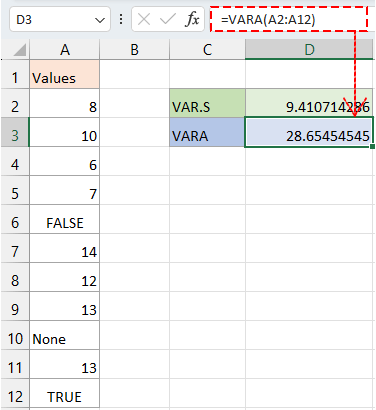
Tarih Saat Hesaplamalarını Hızlandırın
Kutools for Excel'in Tarih Saat Yardımcısı, karmaşık tarih ve saat hesaplamalarını basitleştirmek için tasarlanmış inanılmaz derecede verimli bir araçtır. Deneyin ve veri yönetim deneyiminizi nasıl dönüştürdüğünü görün!
Varyans vs Standart Sapma
Benzerlikler:
Dağılım Ölçüsü:
Hem varyans hem de standart sapma, bir veri setindeki yayılımı veya dağılımı tanımlamak için kullanılan istatistiksel ölçülerdir. Setteki bireysel sayıların ortalamadan (ortalama) ne kadar saptığını nicelendirirler.
Veri Analizi:
Her ikisi de veri değişkenliğini anlamak için istatistiksel analizde yaygın olarak kullanılır. Finans, araştırma, kalite kontrol ve daha birçok alanda gereklidirler.
Ortalamadan Hesaplanır:
Hem varyans hem de standart sapmanın hesaplaması veri setinin ortalaması ile başlar. Bu merkezi değere göre değişkenliği değerlendirirler.
Farklılıklar:
Ölçü Birimleri:
Varyans: Orijinal verilerin karesel birimleri. Örneğin, veriler metre cinsinden ise, varyans metrekare cinsinden olacaktır.
Standart Sapma: Orijinal verilerle aynı birimler. Örneği sürdürürsek, veriler metre cinsinden ise, standart sapma da metre cinsinden olacaktır.
Yorumlama:
Varyans: Orijinal verilerle aynı ölçekte olmadığı için yorumlanması daha az sezgisel olabilen karesel bir tahmin sağlar.
Standart Sapma: Verilerle aynı birimlerde olduğu için daha yorumlanabilir. Veri noktalarının ortalamadan ortalama uzaklığını gösterir.
Matematiksel Tanım:
Varyans: Ortalamadan karelerin farklarının ortalamasıdır.
Standart Sapma: Varyansın kareköküdür.
Uç Değerlere Hassasiyet:
Varyans: Farkları karesi aldığı için uç değerlere daha hassastır.
Standart Sapma: Uç değerlerden etkilenir, ancak karekök nedeniyle varyansa kıyasla daha az hassastır.
Uygulamalar:
Varyans:
Dağılımın karesel büyüklüğüne odaklandığında kullanılır.
Negatif değerleri ortadan kaldırmak için kare alma işleminin gerekli olduğu istatistiksel modeller ve hesaplamalarda faydalıdır.
Risk değerlendirmesi için finansal modellerde sıklıkla kullanılır, çünkü volatiliteyi ölçer.
Standart Sapma:
Raporlarda ve günlük uygulamalarda veri ölçeğiyle doğrudan ilişkili olduğu için daha yaygın kullanılır.
Değişkenliği anlamak için ampirik araştırmalarda gereklidir.
Kalite kontrol, hava raporları ve testlerde standart puanlarda sıklıkla kullanılır.
Sonuç:
Varyans ve standart sapma, bir veri setinin yayılımını ölçmek için hizmet verse de, uygulamaları ölçü birimleri ve yorumlanabilirliklerinden dolayı farklılık gösterir. Verilerin ölçeğiyle doğrudan ilişkili olan standart sapma, özellikle pratik, günlük bağlamlarda daha kullanıcı dostu olma eğilimindedir. Öte yandan, varyans genellikle matematiksel ve istatistiksel modellere daha uygundur.
Bu genel bakış ve karşılaştırma, Excel'de her bir varyans fonksiyonunu ne zaman ve neden kullanacağınız konusunda net bir anlayış sağlamalıdır, böylece daha doğru ve anlamlı veri analizi yapılabilir. Veri yönetimınızı bir üst seviyeye taşıyabilecek daha fazla devrim niteliğindeki Excel stratejileri için buradan keşfetmeye devam edin.
En İyi Ofis Verimlilik Araçları
Kutools for Excel - Kalabalıktan Farklılaşmanızı Sağlar
Kutools for Excel, İhtiyacınız Olan Her Şeyin Bir Tıklama Uzağında Olduğundan Emin Olmak İçin 300'den Fazla Özelliğe Sahiptir...
Office Tab - Microsoft Office'de (Excel Dahil) Sekmeli Okuma ve Düzenlemeyi Etkinleştirin
- Onlarca açık belge arasında bir saniyede geçiş yapın!
- Her gün yüzlerce fare tıklamasından sizi kurtarır, fare eline veda edin.
- Birden fazla belgeyi görüntülediğinizde ve düzenlediğinizde üretkenliğinizi %50 artırır.
- Chrome, Edge ve Firefox gibi Office'e (Excel dahil) Etkin Sekmeler Getirir.
İçindekiler
- Varyans nedir?
- Excel varyans fonksiyonlarına giriş
- Excel'de varyans nasıl hesaplanır?
- VAR.S vs VAR.P – Örnek veya popülasyondan varyans hesaplama
- VAR.S vs VARA – Metinleri ve mantıksal metinleri dahil ederek veya hariç tutarak varyans hesaplama
- Varyans vs Standart sapma
- İlgili Makaleler
- En İyi Ofis Üretkenlik Araçları
- Yorumlar